Auricher Wissenschaftstage –
Forum einer dritten Kultur
Praktikum am ITWM in Kaiserslautern
vom 26. Juni bis zum 24. Juli 2009
Von Vladimir Albach
Im Rahmen der Auricher Wissenschaftstage wurde mir in der Zeit vom 26.06.–24.07.2009 ein Praktikum am Fraunhofer Institut für Techno- und Wirtschaftsmathematik ermöglicht.

Das ITWM
Ich habe in der Abteilung „Optimierung“ an einem Projekt der Chemiefirma BASF mitgearbeitet. An dem Projekt waren auch noch drei Mitarbeiter vom ITWM beteiligt. Es ging darum, die Diskretisierung von Kolonnen (zylinderförmige Rohre) so festzulegen, dass der chemische Prozess, der in der Kolonne statt findet, sich genau abbilden lässt. Zu diesem Zweck gibt es drei mögliche Diskretisierungen in der Kolonne:
horizontal

vertikal
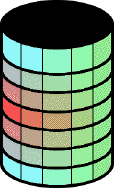
horizontal und vertikal
Ich habe mich mit der vertikalen Diskretisierung beschäftigt. Das Problem ist, dass sich bei der Simulation, je nach Segmenthöhe und Anzahl, die Werte verändern, und man möchte mit möglichst wenigen Segmenten das bestmögliche Ergebnis erzielen. Auch gibt es für die Herleitung der Punkte keine geschlossenen Formeln, vielmehr muss jedes Mal ein großes, komplexes Simulationsprogramm gestartet werden.
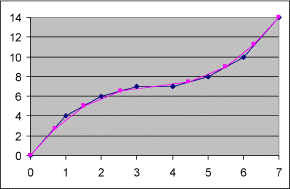
Angeschaut habe ich mir dann hauptsächlich die Temperaturkurven, und so sahen sie ungefähr aus:
Die Referenz-Linie ist eine gleichmäßige Verteilung aus 46 Punkten.
Die äquidistante Linie ist eine gleichmäßige Verteilung aus nur 19 Punkten.
Nun möchte man versuchen, die Punkte so geschickt neu zu verteilen, dass die Kurve mit den 19 Punkten so ähnlich wie möglich aussieht wie die mit den 46 Punkten. Außerdem musste ich auch noch ein wenig die Programmiersprache „Fortran“ lernen, weil das Simulationsprogramm in „Fortran“ geschrieben ist.
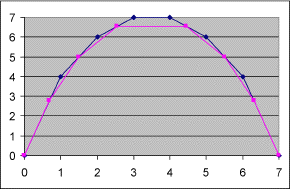
Die erste Verteilungsmöglichkeit, die ich mir angeschaut habe, war die Verteilung auf gleichmäßige Kurvenlängen. Das bedeutet, dass ich versucht habe, den Abstand der einzelnen Punkte zueinander anzugleichen.
Ich erkläre es mal an einem Beispiel:
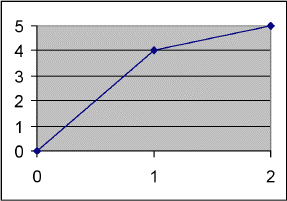
Bei diesen drei Punkten sieht man ganz deutlich, dass die Längen zwischen den Punkten nicht gleichmäßig sind. Trotzdem wäre es schwer, direkt an diesem Beispiel zu arbeiten. Darum habe ich die Punkte normalisiert.
Normalisiert sieht das Ganze dann so aus:
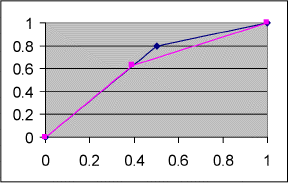
Das Blaue ist die Linie von gerade eben (s. o.) und die rosa Linie ist die, bei der ich die Linien in zwei gleichlange Linien angepasst habe.
Und so sieht die neue Kurve dann aus:
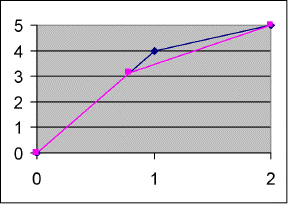
Die Längen sind also nur im normalisierten Graphen gleich. Das hat ganz einfach folgenden Grund: Wenn ich den Graphen nicht normalisieren würde, würde er die Punkte viel zu stark an die Seiten schieben, bei denen der Temperaturunterschied sehr groß ist, denn meistens ist das Intervall für die Temperatur größer als das für die Segmenthöhen. Durch die Normalisierung umgehe ich dieses Problem.
Diese Frage habe ich mir ganz zu Anfang gestellt. Denn abgesehen davon, dass ich dafür sorgen muss, dass die Längen gleich sind, verschiebt mir das Simulationsprogramm nach jedem Neustart die Y-Werte der Punkte wieder ein wenig (natürlich nur wenn ich vorher die Punkte selber etwas verschoben habe).
Das Erste, was ich dann versucht habe, war, dass ich die Punkte in kleinen Einzelschritten so lange bewegt habe, bis die gewünschte Länge erreicht war. Doch das hat so manche Probleme. Abgesehen davon, dass das sehr lange gedauert hätte, musste auch die Schrittweite so gewählt werden, dass die Punkte nicht übereinander springen. Wenn sie es doch täten, könnte es passieren, dass das Simulationsprogramm abstürzt.
Aber das Hauptproblem war einfach die Zeit. Es dauerte viel zu lange (ca. 5–10h).
Deshalb musste ich eine Funktion bauen, die die Position der neuen Punkte schnell berechnet.
Zu diesem Zweck habe ich mir die Durchschnittslänge aller Längen angeschaut und die Punkte dann so lange an der alten Funktion entlang geschoben, bis sie diese Durchschnittslänge erreicht haben. Danach habe ich das Hinschieben nur noch durch eine Formel ersetzt, die die Punkte direkt an ihre neue Position setzt, und fertig war die Funktion, die dann ungefähr so aussah:

Nachdem ich dann endlich eine zeiteffiziente Lösung hatte (nur noch max. 1h – je nach Genauigkeit), durfte ich das Prinzip an einigen Beispielen durchrechnen und dann jeweils die Kurven für Temperatur und die Hauptkomponenten (wie z. B. H2O oder CO2) erstellen, auf denen man sehen konnte, um wie viel ich mich gegenüber der ursprünglichen Äquidistanten verbessert habe. Der Temperaturgraph sah dann ungefähr so aus:
Dadurch, dass die Punkte von der Stelle, an der wenig passiert (oben Mitte), zu den Stellen, an denen mehr passiert (links und rechts), hingeschoben worden sind, sieht die Kurve schon um einiges besser aus.
Die andere Verteilung, die ich mir danach angesehen habe, war die Verteilung auf gleiche Flächen. Die hier in blau dargestellten Flächen sollen gleich groß werden und das sieht man dann in dem Diagramm mit den roten Flächen.
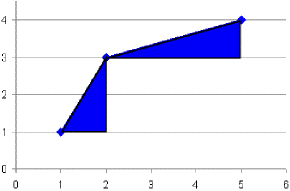
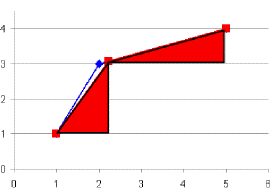
Erst dachte ich, das könne ja nicht so schwer sein, und habe es dann, aufgrund der Ähnlichkeit des Prinzips, genau so gemacht wie bei der Längen-Optimierung. Doch das funktionierte gar nicht, denn im Gegensatz zu den Längen verändern sich die Flächen je nach Ort des Punktes sehr stark. Aber es gab noch ein zweites Problem. Es ist durchaus möglich, dass Folgendes herauskommen kann, wenn die Punkte falsch angesetzt werden:
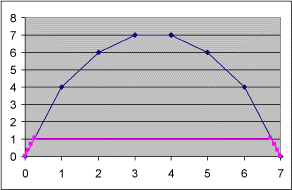
Die rosa Kurve hat ungefähr gleich große Flächen. Doch so sollten die Kurven eigentlich nicht aussehen. Um dieses Problem zu umgehen habe ich die Steigung der Kurve auf eine rein positive geändert. Dadurch konnte bei der Berechnung ein so aussehender Berg nicht mehr einfach durchgeschnitten werden.
Dadurch sah die Kurve dann so aus:
Wenn man die Steigungsänderung nun wieder zurücknehmen würde, hätte man die alte Kurve wieder, nur mit der richtigen Flächenverteilung.
Das einzige Problem, das dadurch entstehen kann, ist, dass bei Kurven wie dieser sich die Fläche im Scheitelpunkt durch die Zurückänderung auf null setzt. Aber da die Fläche in dem Diagramm darüber optimiert worden ist, kann man diese Tatsache ignorieren.
Die Berechnung der neuen Punkte für die Fläche habe ich dann auch durch eine Funktion gelöst, in der die Funktion die Flächen an einen fiktiv orientierten Flächenwert setzt. Da der fiktive Wert selten am Anfang stimmt, betrachte ich mir immer die letzte Fläche. Denn wenn diese Fläche zu klein ist, verkleinere ich den fiktiven Wert, und wenn die Fläche zu groß ist, vergrößere ich ihn. Damit die Berechnung aber auch schnell zu einem Ergebnis kommt, benutzte ich die Intervallhalbierung, denn das geht schnell und ist zuverlässig.
Nachdem ich die Funktion dann endlich fertig hatte, habe ich dieses Prinzip dann noch mal auf alle anderen Beispiele angewandt und wieder die Diagramme erstellt. Das sah dann bei der Temperatur beispielsweise ungefähr so aus:
Der Vorteil bei dieser Verteilung ist, dass sie die Punkte noch stärker an Stellen schiebt, bei der die Steigung im mittleren Bereich liegt (bei 0,45). Der Nachteil ist allerdings, dass diese Verteilung die Punkte an Stellen mit geringer Steigung zu weit auseinander schiebt, sodass dann ein Segment mehrere Meter hoch wäre. Doch dieses Problem kann man beispielsweise durch das Einfügen eines weiteren Punktes schnell lösen.
Auch wenn ich die Mathematik, die hinter der Berechnung der Punkte in der Simulation steht, nicht verstanden habe, so war es doch sehr interessant, mich mit den Problemen der Längenvergleichmäßigung und der Flächenvergleichmäßigung zu beschäftigen und diese dann auch zu lösen. Alleine hätte ich das allerdings nicht geschafft, denn immer wenn mir mal die Ideen ausgingen oder ich einen Fehler gesucht habe und ihn nicht finden konnte, hat mich das Team unterstützt und mir Hilfen und neue Ideen gegeben. Es war für mich also ein sehr schönes Praktikum.
Deswegen möchte ich mich ganz herzlich bei den drei Mitarbeitern des Teams und der ganzen Abteilung „Optimierung“ bedanken, denn alle waren immer für mich da und haben mir alles mit Geduld erklärt. Auch möchte ich mich bei den Auricher Wissenschaftstagen bedanken, dass sie mir dieses Praktikum ermöglicht haben.

Mein Arbeitsplatz am ITWM