Auricher Wissenschaftstage –
Forum einer dritten Kultur
Praktikum am ITWM in Kaiserslautern
vom 4. bis zum 15. August 2008
Von Vladimir Albach
Hier beschreibe ich, was ich während meines Praktikums am Fraunhofer Institut für Techno- und Wirtschaftsmathematik gemacht habe.

Das ITWM
Der Brillant gehört zu den am häufigsten verwendeten Diamantenformen. Nun will ich zeigen, wie man einen Brillanten mit Hilfe von Ebenengleichungen nachbilden kann. Aber erstmal eine kurze Erklärung zu den Ebenengleichungen:
Eine Ebenengleichung sieht wie folgt aus: ax+by+cz+d=0. Für die hier angewandten Ebenengleichungen habe ich jeweils drei Punkte benötigt. Diese Punkte nennt man Vektoren. Da ich im dreidimensionalen Raum arbeite, habe ich für jeden Vektor auch drei Werte: die x-Koordinate, die y-Koordinate und die z-Koordinate.
Um eine Ebene aus drei Punkten zu errechnen, muss man zuerst den Punkt 1 von Punkt 2 abziehen und dann erhält man einen neuen Punkt: Punkt A. Danach zieht man auch den Punkt 1 von Punkt 3 ab und erhält nun Punkt B. Nun nimmt man das Kreuzprodukt aus Punkt A und B. Also Ay*Bz-Az*By=Nx, Az*Bx-Ax*Bz=Ny und Ax*By-Ay*Bx=Nz. Mit dem neuen Punkt N muss dann nur noch durch Einsetzen eines anderen beliebigen Punktes der d-Wert berechnet werden und fertig ist die Ebenengleichung.
Zum Berechnen der weiteren Ebenengleichungen und zum Erstellen des Brillanten habe ich das Programm Mathematica genutzt.
Zuerst muss man wissen, wie ein Brillant aussieht:
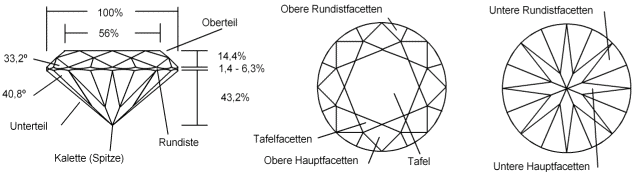
Feinschliff-Brillant (Quelle: Wikipedia)
Den Brillanten kann man demnach in drei Teile unterteilen: Die Krone (der obere Teil), die Rundiste (der „Gürtel“) und den Pavillon (der untere Teil).
Zu allererst habe ich irgendwelche Zahlen genommen um einen Brillanten nachzubilden. Danach habe ich den Brillanten in ein Koordinatensystem gesetzt. Den Ursprung legte ich in die Mitte unterhalb der Rundiste. Die z-Achse zeigt nach oben, die x-Achse nach rechts und die y-Achse in die Tiefe. Jetzt konnte ich beginnen den Pavillon nachzubilden. Zuerst habe ich die acht Hauptfacetten nachgebildet. Die drei Punkte, die ich dafür verwendet habe, waren einmal <0,0,-36> (ganz unten) und dann jeweils zwei nebeneinander liegende Punkte am Rand <x,y,0>, <x,y,0>. Die Formeln sahen am Ende dann wie folgt aus:

Formeln für die acht Hauptfacetten des Brillanten
Nun noch die 16 Rundistfacetten. Den Punkt, in dem sie sich berühren, habe ich erstmal in die Mitte gelegt. Das Problem bei den 16 Rundistfacetten war, dass sie aufgrund der zuvor erstellten Facetten nun nicht mehr bei z=0 lagen sondern etwas versetzt nach oben. Dieses musste ich dann auch berechnen.
Diese 24 berechneten Formeln konnte ich nun zeichnen lassen und heraus kam Folgendes:
Zeichnung des Brillanten (I)
Somit war der Pavillon fertig. Nun konnte ich anfangen die Krone zu berechnen. Dazu habe ich das Gleiche gemacht wie beim Pavillon, nur dass es hier nicht 24 Formeln waren, sondern 33. Nun brauchte ich nur noch die ganzen Formeln zusammenzutun und dann bekam ich folgenden Brillanten heraus:
Zeichnung des Brillanten (II)
Da dies aber eine sehr lange Berechnung erforderte, musste ich das Ganze noch einmal nur mit Variablen erstellen. Nun kann ich aber nicht für jeden Punkt eine Variable erstellen, darum musste ich das Ganze von fünf Variablen abhängig machen: den Durchmesser, den Tafeldurchmesser, die Kronen-Höhe, die Pavillon-Tiefe und die Rundisten-Höhe.
Das Ganze habe ich dann erstmal mit den gleichen Zahlen durchgespielt und die Zuordnung der einzelnen Formeln habe ich dann mithilfe von Schleifen erstellt …
Formel für die Schleifen
… und dann zum Test das Ganze wieder zeichnen lassen:
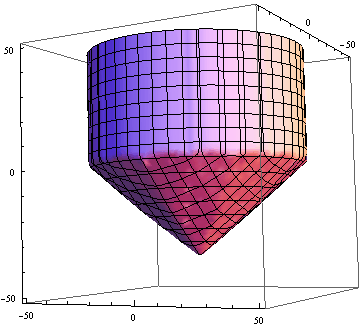
Zeichnung des Brillanten (III)
Nun brauchte ich nur noch die Zahlen durch Variablen zu ersetzen.
Danach durfte ich ein anderes Programm nutzen: Pov-Ray. Hierzu konnte ich Teile der Schleifen-Funktionen übernehmen, um den Brillanten noch einmal zeichnen zu lassen. Dieses mal aber auf höherer Qualität und mit Lichtreflexionen.

Zeichnung des Brillanten (IV)
Nach dem ganzen Zeichnen von Brillanten durfte ich nun eine Formel aufstellen, um das Volumen zu berechnen. Hierfür habe ich mir auch wieder testweise das Zahlenbeispiel genommen, das ich ganz am Anfang verwendet habe.
Zuerst musste ich jedoch den Brillanten wieder stückchenweise berechnen. Vom Pavillon habe ich erstmal ein Achtel genommen und dieses „Kuchenstück“ berechnet. Dafür musste ich das „Kuchenstück“ allerdings wieder in fünf geometrische Figuren aufteilen, die ich dann berechnen konnte. Das von mir berechnete Volumen habe ich dann mit dem Volumen eines Kreiskegels verglichen und dabei habe ich festgestellt, dass das von mir berechnete Volumen um ca. 5% größer war als das Volumen des Kreiskegels. Für das Volumen der Rundiste habe ich dann einfach die Zylinderformel genommen und um die Krone zu berechnen, musste ich die Krone ebenfalls in kleinere geometrische Figuren unterteilen. Verglichen habe ich dann das Ergebnis der Krone mit dem Ergebnis eines Kreiskegelstumpfes und hier ist der Unterschied sehr gering.
Nun konnte ich wieder Variablen statt Zahlen einsetzen und daraus entstand dann folgende Volumenformel: V =
Volumen-Formel
Zusätzlich kann man den Brillanten noch variieren. Man kann nämlich beim Pavillon und bei der Krone den Punkt, an dem sich die Ebenen treffen, verschieben. Somit entstehen leicht veränderte Formeln z. B. für das Volumen.
Und hier noch ein paar Bilder von Brillanten, die ich erstellt habe.





















Das Fraunhofer-Institut versucht damit, aus Rohedelsteinen beim Schleifen durch Verwenden der am besten passenden Form das maximale Volumen herauszuholen.

Am Arbeitsplatz im ITWM